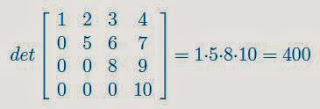Właściwe podejście do rozwoju osobistego i nauki: WIDEO + 5 wskazówek

Dziś publikuję artykuł zawierający film wideo oraz kilka moich porad o tym jak uczyć się matematyki szybciej, skuteczniej i na dłużej zapamiętać materiał.

Oto obiecany filmik, który powinien pomóc Ci w poprawieniu Twojego podejścia do rozwoju i nauki matematyki i wiele więcej:-)
Miłego oglądania.

Jako bonus kilka moich porad o podejściu do nauki.

1. Zanim zaczniesz naukę, postaw sobie jasno określony, precyzyjny cel - Po co się tego będę uczyć?

2. Określ co jest niezbędne do nauczenia się danego materiału, np. do nauczenia się obliczania wyznacznika macierzy trzeba znać podstawowe pojęcia i do tego oczywiście wzory...

3. Rozkładaj skomplikowane zagadnienia na mniejsze, łatwiejsze do zrozumienia schematy, np. liczenie macierzy odwrotnej ze wzoru można podzielić na trzy mniejsze kroki:

(a) liczymy wyznacznik macierzy i sprawdzamy, czy jest różny od zera (macierz nieosobliwa)
(b) liczymy dopełnienia algebraiczne wszystkich elementów macierzy
(c) tworzymy macierz dopełnień, mnożymy ją przez odwrotność wyznacznika i transponujemy

4. Pracuj systematycznie, małymi kroczkami dojdziesz na szczyt (tak jak opisał to Mirek w filmie wideo). Lepiej robić jeden przykład dziennie przez miesiąc niż próbować opanować cały materiał w ciągu jednego dnia...

5. Korzystaj z pomocy naukowych online, skryptów itp. Sprawdź moje dwie strony pomocne w nauce matematyki wyższej  orzelzmatmy.pl i obliczone.pl

Od Ciebie zależy jak wdrożysz te wszystkie porady w swoim życiu. Naprawdę warto :-)
Napisz w komentarzu poniżej jak Ci się udało.
Masz jakieś swoje megasposoby na naukę liczb zespolonych i matematyki? Czekam na Twoje pomysły.

Wyznacznik macierzy 4x4... Czasem da się policzyć w 10 sekund!

Czasami liczenie wyznacznika macierzy stopnia 4 może być bardzo proste:-)
Np. gdy macierz jest trójkątna (ma niezerowe elementy tylko na przekątnej oraz powyżej lub poniżej przekątnej) lub diagonalna, wtedy wyznacznik jest równy iloczynowi liczb leżących na przekątnej...

Oto przykład:

Powyższy wyznacznik liczymy mnożąc liczby: 1, 5, 8, 10. 
Więcej tego typu przydatnych trików z macierzy znajdziecie na stronie http://obliczone.pl/zadania/macierze

Wyznacznik macierzy do potęgi - jak to policzyć?

Zobaczcie ciekawe zadanie dotyczące obliczania wyznacznika macierzy. Nietypowe jest to, że macierz jest podniesiona do wysokiej potęgi... Jak to policzyć? Wystarczy zastosować bardzo użyteczną własność wyznacznika:)

Więcej tego typu pouczających zadań z macierzy i nie tylko znajdziecie na stronie Obliczone.pl

Zadania z rozwiązaniami z macierzy i wyznaczników

Pewnie doskonale zdajesz sobie sprawę, że sama nauka teorii z zakresu macierzy nie wystarczy, bo na kolokwiach i egzaminach sprawdzana jest umiejętność rozwiązywania zadań.

Jak szybko i bez żadnych ćwiczeń zwiększyć swoją koncentrację i zdolności umysłowe?
 
Nawet doskonała znajomość teorii nie zagwarantuje Ci zdanego kolokwium, chociaż na pewno bardzo ułatwi zrozumienie schematów rozwiązywania zadań.

Jeśli zastanawiasz się jak nauczyć się rozwiązywać zadania to zobacz jak uczyć się matematyki.
Następnie zobacz rewelacyjną stronę internetową zawierającą zadania z matematyki z rozwiązaniami.

Jeśli masz zbyt duże braki z matematyki, żeby samodzielnie przedzierać się przez rozwiązania zadań, to polecam kurs macierzy.

Zapamiętaj:
Żeby nauczyć się rozwiązywać zadania, nie wystarczy nauczyć się na pamięć kilku schematów, trzeba to po prostu zrozumieć:-)
  
Jeśli znasz inne strony internetowe pomocne w nauce macierzy, to podziel się tym z innymi! Bloga ogląda kilkaset osób dziennie i na pewno będą Ci za to wdzięczni:-)  

Jaka jest różnica między macierzą jednostkową a diagonalną?

W tym poście postaram się odpowiedzieć na pytanie, jaka jest różnica między macierzą diagonalną a jednostkową?
Na początek chcę polecić Ci powtórkę z rodzajów macierzy dostępną na tym blogu (Jak się nauczyć macierzy w pół godziny?), warta polecenia jest też powtórka na stronie o rodzajach macierzy.

Ogólnie możemy powiedzieć, że macierz jednostkowa to macierz kwadratowa, posiadająca jedynki (1) na głównej przekątnej a poza przekątną same zera.

Macierz diagonalna z kolei to macierz posiadająca zera poza główną przkątną (na przekątnej mogą stać dowolne liczby, również zera). 

Stąd wniosek, że macierz jednostkowa to macierz diagonalna posiadająca jedynki (1) na przekątnej. 

Inne przykładem macierzy diagonalnej jest kwadratowa macierz zerowa. Taka macierz jest diagonalna, poniważ posiada zera poza przekątną (i zera na przekątnej ale to w niczym nie przeszkadza).

Jeśli masz jakieś pytania o rozdzaje macierzy to zapraszam do pozostawienia go pod tym postem.

Spektakularne zastosowania macierzy

Jeśli zastanawiasz się po co wymyślono macierze, to dobrze trafiłeś(-aś). Poniżej znajdziesz kilkanaście przykładów zastosowań macierzy. UWAGA: będą to przykłady naprawdę spektakularne... Dowiesz się m.in. co wspólnego ma firma Google z macierzami oraz jak wykonuje się prognozy pogody?

Zacznijmy od początku...

Macierze, bo o nich tu mowa, wymyślono przede wszystkim w celu szybkiego rozwiązywania skomplikowanych układów równań liniowych, tzn. układów w których jest wiele niewiadomych i występuje wiele równań. (jeśli nie wiesz co to jest ten cały układ równań, to zobacz tutaj).

Oto lista pojęć związanych z macierzami wraz z wytłumaczeniem, co konkretnie można za ich pomocą osiągnąć:

•  działania na macierzach: dodawanie i odejmowanie, mnożenie i transpozycja - za pomocą macierzy (oraz operacji na nich) można zapisać każdy układ równań
• wyznacznik macierzy - służy do znajdowania macierzy odwrotnej oraz rozwiązywania układów równań za pomocą wzorów Cramera
• rząd macierzy - wraz z twierdzeniem Kroneckera-Capellego pozwala określić ile rozwiązań ma układ równań liniowych

Cała teoria macierzy, wszystkie pojęcia i schematy wymyślono w celu ułatwienia rozwiązywania układów równań, które z kolei służą do opisu wielu zjawisk rzeczywistych, np.:

• w fizyce do opisu ruchu 2 lub większej ilości ciał oddziałujących na siebie
• w  meteorologii do opisu zjawisk fizycznych i procesów zachodzących w atmosferze. Prognozy pogody przeprowadza się rozwiązując skomplikowane układy równań, które stanowią zapis za pomocą równań pewnych zależności między parametrami opisującymi stan pogody (tj. temperatura, ciśnienie, wilgotność, siła wiatru itd.) w danej chwili. Rozwiązanie układu w zależności od warunków początkowych umożliwia określenie parametrów pogodowych w przyszłości.
• w ekonomii, do opisu zjawisk takich jak inflacja czy wzrost kapitału
• w każdej dziedzinie w której pojawia się problem optymalizacji (minimalizacji lub maksymalizacji) jakichś wielkości lub występują zjawiska o skomplikowanej naturze (wiele czynników wpływających na zjawisko oraz wiele zależności między tymi czynnikami)

Oprócz zastosowań do rozwiązywania układów równań, macierze stosowane są w wielu innych dzidzinach, np.:

• do zapisywania dużych zbiorów danych, które są we wzajemnej relacji. Szczególnie ważną rolę pełnią macierze w informatyce oraz statystyce, gdzie często występują ogromne zbiory danych (wyniki pomiarów, dane w pamięci komputera itd.). 
• co ciekawe za pomocą macierzy modeluje się ekran komputera, który składa się z milionów pikseli ułożonych w sposób logiczny w wierszach i kolumnach, dzięki temu możemy korzystać z komputera, telewizora czy telefonu

Spektakularnym przykładem zastosowań macierzy w informatyce są wyszukiwarki internetowe, wśród których najpopularniejsza jest ta od firmy Google. Wyszukiwarka Google przyporządkowuje stronom internetowym pewien wskaźnik, którego początekiem był tzw. PageRank (PR). W skrócie można to opisać tak: im wyższy PR tym strona wyżej pojawia się w wyszukiwarce. Wartość PR nadawana jest w oparciu o ilość (i jakość) linków prowadzących do danej strony www. W algorytmie PR wykorzystywane są macierze i tzw. wartości i wektory własne macierzy, więcej w 2 artykułach (w j. angielskim):

Algorytm PageRank, czyli jak działa wyszukiwarka

Wektor własny i algebra liniowa stoją za sukcesem Google

UWAGA: Artykuł pochodzi ze strony macierze.bloog.pl

Jaka jest różnica między wierszem a kolumną macierzy?

Jeśli masz problem z zapamiętaniem czym jest wiersz a czym kolumna macierzy, to ten post jest właśnie dla Ciebie:-)!

Co to jest wiersz macierzy?

Wiersz macierzy to pozioma linia (na rysunku poniżej 2 wiersz zaznaczony jest kolorem zielono-niebieskim), na której obok siebie znajdują się kolejne elementy macierzy:

Co to jest kolumna macierzy?

Kolumna to pionowa linia na której leżą elementy macierzy jeden pod drugim (na rysunku poniżej 1 kolumna macierzy jest zaznaczona kolorem czerwonym):

Prawda, że proste? Wiersz i kolumna macierzy to jedne z najbardziej podstawowych pojęć na algebrze liniowej. W filmie poniżej możesz zapoznać się z podstawowymi zagadnieniami z zakresu macierzy:

Jak zwykle zachęcam do zadawania pytań na temat macierzy i nie tylko w komentarzach pod tym postem.