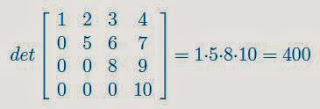Wyznacznik macierzy 4x4... Czasem da się policzyć w 10 sekund!

Czasami liczenie wyznacznika macierzy stopnia 4 może być bardzo proste:-)
Np. gdy macierz jest trójkątna (ma niezerowe elementy tylko na przekątnej oraz powyżej lub poniżej przekątnej) lub diagonalna, wtedy wyznacznik jest równy iloczynowi liczb leżących na przekątnej...

Oto przykład:

Powyższy wyznacznik liczymy mnożąc liczby: 1, 5, 8, 10. 
Więcej tego typu przydatnych trików z macierzy znajdziecie na stronie http://obliczone.pl/zadania/macierze

Wyznacznik macierzy do potęgi - jak to policzyć?

Zobaczcie ciekawe zadanie dotyczące obliczania wyznacznika macierzy. Nietypowe jest to, że macierz jest podniesiona do wysokiej potęgi... Jak to policzyć? Wystarczy zastosować bardzo użyteczną własność wyznacznika:)

Więcej tego typu pouczających zadań z macierzy i nie tylko znajdziecie na stronie Obliczone.pl

Macierze - 3 najważniejsze schematy

Dzisiaj pokażę Ci 3 najważniejsze schematy z zakresu macierzy. Schematy te są naprawdę niezbędne do zdania algebry liniowej na studiach. Zaczynamy...

Schemat 1 - Mnożenie macierzy

Jest to chyba najważniejszy schemat, ponieważ przydaje się w zadaniach typu:

• wykonaj działania na macierzach (takie zadanie pojawia się na kolokwiach prawie zawsze)
• rozwiąż układ równań (mnożenie macierzy służy do zapisywania układów za pomocą macierzy)
• oblicz wartości i wektory własne

Tutaj znajdziesz schemat mnożenia macierzy.
  
Schemat 2 - Obliczanie wyznacznika macierzy

Ważny schemat ze względu na to, że:

• wyznacznik jest niezbędny przy liczeniu macierzy odwrotnej
• jest niezbędny przy rozwiązywaniu układów równań

Tutaj znajdziesz schemat obliczania wyznacznika macierzy.

Schemat 3 - Obliczanie macierzy odwrotnej

3 bardzo ważny schemat, który pojawia się w zadaniach typu: 

• oblicz macierz odwrotną 
• rozwiąż układ równań liniowych

Tutaj znajdziesz schemat obliczania macierzy odwrotnej.

Znając 3 powyżej opisane schematy będziesz w stanie zdać każde kolokwium lub egzamin. Ucząc się materiału z zakresu macierzy warto skupić się na tych schematach, ćwiczyć i rozwiązywać konkretne zadania. To prawdziwy klucz do sukcesu! Jeśli masz jakieś pytania to napisz w komentarzu pod tym postem - chętnie Ci pomogę:-) 

Metody obliczania wyznacznika macierzy

Wyznacznik macierzy to chyba najważniejsze z pojęć pojawiających się na algebrze. Z wyznacznikiem spotkasz się najczęściej w następujących problemach:

• odwracanie macierzy
• rozwiązywanie układu równań liniowych
• sprawdzanie czy macierz jest osobliwa czy też nieosobliwa
• obliczanie pola lub objętości bryły
• zamiana zmiennych w całkach wielokrotnych
• sprawdzanie czy układ rozwiązań jest fundamentalny (równania różniczkowe)

Na tym blogu znajdziesz tylko wstęp do różnych pojęć matematycznych, więcej możesz nauczyć się na moich stronach matematycznych http://orzelzmatmy.pl oraz http://obliczone.pl

Metody obliczania wyznacznika - teoria

Znane są dwie ogólne metody obliczania wyznacznika macierzy:

1. Metoda Laplace'a (lub inaczej rozwinięcie Laplacea) - metoda ta polega na uproszczeniu obliczeń wyznacznika poprzez rozbicie go na sumę wyznaczników macierzy mniejszego stopnia. Polega to na tym, że wybieramy sobie wiersz lub kolumnę zawierającą dużą ilość zer, następnie mnożymy każdy element wybranego wiersza lub kolumny przez dopełnienie algebraiczne tego elementu. Na koniec dodajemy do siebie wszystkie liczby i w ten sposób obliczamy wyznacznik. Metoda ta jest czasochłonna ale działa zawsze i dla każdej macierzy kwadratowej.
2. Operacje elementarne na wierszach i kolumnach macierzy (eliminacja Gaussa) - metoda ta polega na wykonywaniu operacji elementarnych w celu uproszczenia obliczeń wyznacznika. Dozwolone operacje to: 1. Dodanie wielokrotności jednego wiersza (kolumny) do innego wiersza (kolumny) - nie zmienia wartości wyznacznika. 2. Pomnożenie wiersza (kolumny) przez liczbę powoduje pomnożenie wyznacznika przez tę liczbę. 3. Zamiana miejscami dwóch wierszy, tak jak i zamiana miejscami dwóch kolumn, zmienia znak wyznacznika na przeciwny (plus na minus, minus na plus). Metoda przez operacje elementarne wymaga dużej wprawy i biegłości - dlatego jej stosowanie polecam bardziej zaawansowanym osobom.
3. Metoda mieszana, polegająca na wykorzystaniu operacji elementarnych i/lub rozwinięcia Laplacea, Polega to na tym, że np. stosujemy najpierw rozwinięcie Laplacea i potem dopiero używamy operacji elementarnych w celu uproszczenia obliczeń wyznaczników, które powstały w wyniku użycia metody Laplacea. Ta metoda jest bardzo użyteczna, ponieważ zapewnia dużą elastyczność. Możesz ją stosować do rozwiązywania zadań w których nie jest napisane jaką metodą należy obliczyć wyznacznik macierzy.
4. Metody szczególne - szybki wzorek na obliczanie wyznacznika macierzy wymiaru 2x2 (mnożenie elementów po przekątnej i odjęcie tak uzyskanych iloczynów) oraz metoda Sarrusa pozwalająca w łatwy sposób obliczyć wyznacznik macierzy wymiaru 3x3.

Dość teorii teraz czas na praktykę, czyli konkretne przykłady...

Metody liczania wyznacznika w praktyce

Rozwinięcia Laplacea

Operacje elementarne

wkrótce

Metoda Sarrusa

Wyznacznik macierzy 2x2

Jeśli masz problem z obliczeniem jakiegoś wyznacznika, to pisz śmiało w komentarzu pod tym postem - postaram się pomóc:-)